Introduction

Converting between mass and moles is one of the most frequently encountered skills in chemistry. While the mole concept (Lecture 2) and molar mass (Lecture 3) provide the foundation, the ability to switch fluidly between grams and moles is essential for laboratory work, stoichiometric calculations, and solution preparation.

In this lecture, we will cover:

1. The relationship between mass, moles, and molar mass
2. Step-by-step methods for conversions
3. Worked examples with increasing complexity
4. Converting particles to moles and vice versa
5. Common errors and how to avoid them
6. Practical applications in the laboratory and industry

By the end of this lecture, students will have the tools to solve any mass-mole conversion problem accurately.

1. The Fundamental Relationship

The relationship between mass (m), number of moles (n), and molar mass (M) is expressed as:

n = m ÷ M

Where:

• n = number of moles (mol)
• m = mass of the substance (g)
• M = molar mass (g/mol)

This formula is fundamental for most quantitative chemistry calculations.

2. Step-by-Step Conversion Methods

2.1 Converting Mass to Moles

Step 1: Determine the molar mass of the substance using the periodic table.

Step 2: Measure the mass of the substance in grams.

Step 3: Apply the formula:

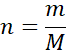
Step 4: Include units and significant figures.

Example 1:
Calculate the number of moles in 20 g of CO₂.

Solution:

• Molar mass of CO₂ = 12 + (16 × 2) = 44 g/mol
• Mass = 20 g
• Number of moles = mass ÷ molar mass = 20 ÷ 44 ≈ 0.455 moles

2.2 Converting Moles to Mass

Step 1: Determine the number of moles (n) of the substance.

Step 2: Determine the molar mass (M) from the periodic table.

Step 3: Apply the formula:

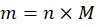
Step 4: Express the answer in grams with appropriate significant figures.

Example 2:
Find the mass of 0.75 moles of NaCl.

Solution:

1. Molar mass NaCl = 22.99 + 35.45 = 58.44 g/mol
2. Mass = 0.75 × 58.44 ≈ 43.83 g

2.3 Converting Particles to Moles

The number of particles (atoms, molecules, ions) can be converted to moles using Avogadro’s number:

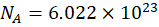
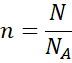
Example 3:
How many moles are in 1.204 × 10²⁴ molecules of O₂?

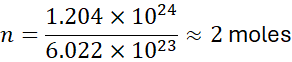
2.4 Converting Moles to Particles

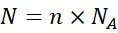
Example 4:
Calculate the number of water molecules in 0.5 moles of H₂O.

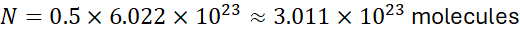
3. Worked Examples with Increasing Complexity

Example 5: Mass of Compound from Moles

Problem: Calculate the mass of 0.25 moles of glucose (C₆H₁₂O₆).

Solution:

1. Molar mass of C₆H₁₂O₆ = 180.16 g/mol
2. Mass = 0.25 × 180.16 ≈ 45.04 g

Example 6: Moles of a Hydrated Salt

Problem: How many moles are in 24.97 g of CuSO₄·5H₂O?

Solution:

1. Molar mass = 249.7 g/mol
2. Moles = 24.97 / 249.7 ≈ 0.1 mol

Example 7: Number of Atoms in a Sample

Problem: How many oxygen atoms are in 18 g of water?

Solution:

1. Moles of H₂O = 18 / 18 ≈ 1 mol
2. Each molecule has 1 oxygen atom
3. Number of oxygen atoms = 1 × 6.022 × 10²³ ≈ 6.022 × 10²³ atoms

Example 8: Particles in a Mass of Sodium

Problem: Calculate the number of sodium atoms in 46 g of Na.

Solution:

1. Molar mass of Na = 22.99 g/mol
2. Moles = 46 / 22.99 ≈ 2.0 mol
3. Number of atoms = 2.0 × 6.022 × 10²³ ≈ 1.204 × 10²⁴ atoms

Example 9: Mixture of Compounds

Problem: A sample contains 10 g of NaCl and 5 g of Na₂SO₄. Calculate the total moles of sodium.

Solution:

• NaCl: 10 g / 58.44 g/mol ≈ 0.171 mol Na
• Na₂SO₄: 5 g / 142.04 g/mol ≈ 0.0352 mol compound → 0.0704 mol Na
• Total moles of Na ≈ 0.2414 mol

Example 10: Mass of Gas Using Moles

Problem: Calculate the mass of 3.0 moles of O₂.

Solution:

1. Molar mass O₂ = 32 g/mol
2. Mass = 3 × 32 = 96 g

4. Practical Applications

4.1 Laboratory Applications

• Determining reactant quantities for reactions
• Calculating yields and limiting reagents
• Preparing solutions of specified molarity

Example: Preparing 250 mL of 0.5 M NaOH:

4.2 Industrial Applications

• Scaling chemical reactions for production
• Ensuring precise dosing in pharmaceuticals
• Optimising the raw material used to reduce waste

5. Common Pitfalls and Errors

1. Unit mismatch: Mass must be in grams, molar mass in g/mol
2. Ignoring molecular structure: O₂ vs O atoms
3. Hydrates: Include water of crystallisation
4. Significant figures: Maintain precision throughout calculations
5. Mixtures: Calculate each component separately

6. Practical Tips

• Always start by writing what is given and what is required
• Use conversion trees: mass ↔ moles ↔ particles
• Double-check atomic masses from the periodic table
• Include units at every step to reduce errors

Further Reading:

• ChemCollective – Mole Calculations

Conclusion

Converting between mass and moles is a critical skill in quantitative chemistry. Mastery of these conversions allows students and chemists to:

• Predict reaction yields
• Prepare solutions accurately
• Determine the number of atoms or molecules in a sample
• Apply these calculations to laboratory and industrial settings

Subsequent lectures will build on this foundation to explore solution concentrations, percentage composition, empirical formulas, and chemical equation balancing, culminating in comprehensive worked examples.

Next Lecture (Lecture 5): Concentration of Solutions – Molarity, Dilutions, and Applications.

Support the Archive

This archive is freely shared as a communal act of care.

If you’d like to support its continuation, consider purchasing a companion PDF set for £1 per lecture, with an associated quiz, via Payhip, with the final price depending on the number of lectures in the set, available only once the full series is complete.

Explore more with us:

• Read our Informal Blog for relaxed insights
• Discover Deconvolution and see what’s happening
• Visit Gwenin for a curated selection of frameworks
• Browse Spiralmore collections